Archive for Juli 2017
Hukum Newton 1,2,3
ENJOYY😄😄
langsung nih artikelnya
Hukum gerak Newton adalah tiga hukum fisika yang menjadi dasar mekanika klasik. Hukum ini menggambarkan hubungan antara gaya yang bekerja pada suatu benda dan gerakyang disebabkannya. Hukum ini telah dituliskan dengan pembahasaan yang berbeda-beda selama hampir 3 abad,[1] dan dapat dirangkum sebagai berikut:
Hukum Pertama: setiap benda akan memiliki kecepatan yang konstan kecuali ada gaya yang resultannya tidak nol bekerja pada benda tersebut.[2][3][4] Berarti jika resultan gaya nol, maka pusat massa dari suatu benda tetap diam, atau bergerak dengan kecepatan konstan (tidak mengalami percepatan). Hal ini berlaku jika dilihat dari kerangka acuan inersial.
Hukum Kedua: sebuah benda dengan massa M mengalami gaya resultan sebesar F akan mengalami percepatan a yang arahnya sama dengan arah gaya, dan besarnya berbanding lurus terhadap F dan berbanding terbalik terhadap M. atau F=Ma. Bisa juga diartikan resultan gaya yang bekerja pada suatu benda sama dengan turunan dari momentum linear benda tersebut terhadap waktu.
Hukum Ketiga: gaya aksi dan reaksi dari dua benda memiliki besar yang sama, dengan arah terbalik, dan segaris. Artinya jika ada benda A yang memberi gaya sebesar F pada benda B, maka benda B akan memberi gaya sebesar –F kepada benda A. F dan –F memiliki besar yang sama namun arahnya berbeda. Hukum ini juga terkenal sebagai hukum aksi-reaksi, dengan F disebut sebagai aksi dan –F adalah reaksinya.
Ketiga hukum gerak ini pertama dirangkum oleh Isaac Newton dalam karyanya Philosophiæ Naturalis Principia Mathematica, pertama kali diterbitkan pada 5 Juli 1687.[5] Newton menggunakan karyanya untuk menjelaskan dan meniliti gerak dari bermacam-macam benda fisik maupun sistem.[6] Contohnya dalam jilid tiga dari naskah tersebut, Newton menunjukkan bahwa dengan menggabungkan antara hukum gerak dengan hukum gravitasi umum, ia dapat menjelaskan hukum pergerakan planet milik Kepler.
Hukum pertama Newton[sunting | sunting sumber]
Berkas:First law.ogv
Walter Lewin menjelaskan hukum pertama Newton.(MIT Course 8.01)[10]
Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Hukum I: Setiap benda akan mempertahankan keadaan diam atau bergerak lurus beraturan, kecuali ada gaya yang bekerja untuk mengubahnya.[11]
Hukum ini menyatakan bahwa jika resultan gaya (jumlah vektor dari semua gaya yang bekerja pada benda) bernilai nol, maka kecepatan benda tersebut konstan. Dirumuskan secara matematis menjadi:
{\displaystyle \sum \mathbf {F} =0\Rightarrow {\frac {d\mathbf {v} }{dt}}=0.}
Artinya :
Sebuah benda yang sedang diam akan tetap diam kecuali ada resultan gaya yang tidak nol bekerja padanya.
Sebuah benda yang sedang bergerak, tidak akan berubah kecepatannya kecuali ada resultan gaya yang tidak nol bekerja padanya.
Hukum pertama newton adalah penjelasan kembali dari hukum inersia yang sudah pernah dideskripsikan oleh Galileo. Dalam bukunya Newton memberikan penghargaan pada Galileo untuk hukum ini. Aristotelesberpendapat bahwa setiap benda memilik tempat asal di alam semesta: benda berat seperti batu akan berada di atas tanah dan benda ringan seperti asap berada di langit. Bintang-bintang akan tetap berada di surga. Ia mengira bahwa sebuah benda sedang berada pada kondisi alamiahnya jika tidak bergerak, dan untuk satu benda bergerak pada garis lurus dengan kecepatan konstan diperlukan sesuatu dari luar benda tersebut yang terus mendorongnya, kalau tidak benda tersebut akan berhenti bergerak. Tetapi Galileo menyadari bahwa gaya diperlukan untuk mengubah kecepatan benda tersebut (percepatan), tetapi untuk mempertahankan kecepatan tidak diperlukan gaya. Sama dengan hukum pertama Newton : Tanpa gaya berarti tidak ada percepatan, maka benda berada pada kecepatan konstan.
Hukum kedua Newton[sunting | sunting sumber]
Walter Lewin menjelaskan hukum dua nuwton menggunakan gravitasi pada contohnya.
(MIT OCW)[12]
Hukum kedua menyatakan bahwa total gaya pada sebuah partikel sama dengan banyaknya perubahan momentum linier p terhadap waktu :
{\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}},}
Karena hukumnya hanya berlaku untuk sistem dengan massa konstan,[13][14][15] variabel massa (sebuah konstan) dapat dikeluarkan dari operator diferensialdengan menggunakan aturan diferensiasi. Maka,
{\displaystyle \mathbf {F} =m\,{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}=m\mathbf {a} ,}
Dengan F adalah total gaya yang bekerja, m adalah massa benda, dan a adalah percepatan benda. Maka total gaya yang bekerja pada suatu benda menghasilkan percepatan yang berbanding lurus.
Massa yang bertambah atau berkurang dari suatu sistem akan mengakibatkan perubahan dalam momentum. Perubahan momentum ini bukanlah akibat dari gaya. Untuk menghitung sistem dengan massa yang bisa berubah-ubah, diperlukan persamaan yang berbeda.
Sesuai dengan hukum pertama, turunan momentum terhadap waktu tidak nol ketika terjadi perubahan arah, walaupun tidak terjadi perubahan besaran. Contohnya adalah gerak melingkar beraturan. Hubungan ini juga secara tidak langsung menyatakan kekekalan momentum: Ketika resultan gaya yang bekerja pada benda nol, momentum benda tersebut konstan. Setiap perubahan gaya berbanding lurus dengan perubahan momentum tiap satuan waktu.
Hukum kedua ini perlu perubahan jika relativitas khusus diperhitungkan, karena dalam kecepatan sangat tinggi hasil kali massa dengan kecepatan tidak mendekati momentum sebenarnya.
Impuls[sunting | sunting sumber]
Impuls J muncul ketika sebuah gaya F bekerja pada suatu interval waktu Δt, dan dirumuskan sebagai[16][17]
{\displaystyle \mathbf {J} =\int _{\Delta t}\mathbf {F} \,\mathrm {d} t.}
Impuls adalah suatu konsep yang digunakan untuk menganalisis tumbukan.[18]
Sistem dengan massa berubah[sunting | sunting sumber]
Sistem dengan massa berubah, seperti roket yang bahan bakarnya digunakan dan mengeluarkan gas sisa, tidak termasuk dalam sistem tertutup dan tidak dapat dihitung dengan hanya mengubah massa menjadi sebuah fungsi dari waktu di hukum kedua.[14] Alasannya, seperti yang tertulis dalam An Introduction to Mechanics karya Kleppner dan Kolenkow, adalah bahwa hukum kedua Newton berlaku terhadap partikel-partikel secara mendasar.[15] Pada mekanika klasik, partikel memiliki massa yang konstant. Dalam kasus partikel-partikel dalam suatu sistem yang terdefinisikan dengan jelas, hukum Newton dapat digunakan dengan menjumlahkan semua partikel dalam sistem:
{\displaystyle \mathbf {F} _{\mathrm {total} }=M\mathbf {a} _{\mathrm {pm} }}
dengan Ftotal adalah total gaya yang bekerja pada sistem, M adalah total massa dari sistem, dan apm adalah percepatan dari pusat massa sistem.
Sistem dengan massa yang berubah-ubah seperti roket atau ember yang berlubang biasanya tidak dapat dihitung seperti sistem partikel, maka hukum kedua Newton tidak dapat digunakan langsung. Persamaan baru digunakan untuk menyelesaikan soal seperti itu dengan cara menata ulang hukum kedua dan menghitung momentum yang dibawa oleh massa yang masuk atau keluar dari sistem:[13]
{\displaystyle \mathbf {F} +\mathbf {u} {\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}}
dengan u adalah kecepatan dari massa yang masuk atau keluar relatif terhadap pusat massa dari objek utama. Dalam beberapa konvensi, besar (u dm/dt) di sebelah kiri persamaan, yang juga disebut dorongan, didefinisikan sebagai gaya (gaya yang dikeluarkan oleh suatu benda sesuai dengan berubahnya massa, seperti dorongan roket) dan dimasukan dalam besarnya F. Maka dengan mengubah definisi percepatan, persamaan tadi menjadi
{\displaystyle \mathbf {F} =m\mathbf {a} .}
Hukum ketiga Newton[sunting | sunting sumber]
Hukum Ketiga Newton. Para pemain sepatu luncur es memberikan gaya pada satu sama-lain dengan besar yang sama tetapi berlawanan arah.
Berkas:Thirdlaw.ogv
Penjelasan hukum ketiga Newton.[19]
“ Lex III: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi. ”
“ Hukum ketiga : Untuk setiap aksi selalu ada reaksi yang sama besar dan berlawanan arah: atau gaya dari dua benda pada satu sama lain selalu sama besar dan berlawanan arah. ”
Benda apapun yang menekan atau menarik benda lain mengalami tekanan atau tarikan yang sama dari benda yang ditekan atau ditarik. Kalau anda menekan sebuah batu dengan jari anda, jari anda juga ditekan oleh batu. Jika seekor kuda menarik sebuah batu dengan menggunakan tali, maka kuda tersebut juga "tertarik" ke arah batu: untuk tali yang digunakan, juga akan menarik sang kuda ke arah batu sebesar ia menarik sang batu ke arah kuda.
Hukum ketiga ini menjelaskan bahwa semua gaya adalah interaksi antara benda-benda yang berbeda,[20] maka tidak ada gaya yang bekerja hanya pada satu benda. Jika benda A mengerjakan gaya pada benda B, benda B secara bersamaan akan mengerjakan gaya dengan besar yang sama pada benda A dan kedua gaya segaris. Seperti yang ditunjukan di diagram, para peluncur es (Ice skater) memberikan gaya satu sama lain dengan besar yang sama, tetapi arah yang berlawanan. Walaupun gaya yang diberikan sama, percepatan yang terjadi tidak sama. Peluncur yang massanya lebih kecil akan mendapat percepatan yang lebih besar karena hukum kedua Newton. Dua gaya yang bekerja pada hukum ketiga ini adalah gaya yang bertipe sama. Misalnya antara roda dengan jalan sama-sama memberikan gaya gesek.
Secara sederhananya, sebuah gaya selalu bekerja pada sepasang benda, dan tidak pernah hanya pada sebuah benda. Jadi untuk setiap gaya selalu memiliki dua ujung. Setiap ujung gaya ini sama kecuali arahnya yang berlawanan. Atau sebuah ujung gaya adalah cerminan dari ujung lainnya.
Secara matematis, hukum ketiga ini berupa persamaan vektor satu dimensi, yang bisa dituliskan sebagai berikut. Asumsikan benda A dan benda B memberikan gaya terhadap satu sama lain.
{\displaystyle \sum \mathbf {F} _{a,b}=-\sum \mathbf {F} _{b,a}}
Dengan
Fa,b adalah gaya-gaya yang bekerja pada A oleh B, dan
Fb,a adalah gaya-gaya yang bekerja pada B oleh A.
Newton menggunakan hukum ketiga untuk menurunkan hukum kekekalan momentum,[21] namun dengan pengamatan yang lebih dalam, kekekalan momentum adalah ide yang lebih mendasar (diturunkan melalui teorema Noether dari relativitas Galileo dibandingkan hukum ketiga, dan tetap berlaku pada kasus yang membuat hukum ketiga newton seakan-akan tidak berlaku. Misalnya ketika medan gaya memiliki momentum, dan dalam mekanika kuantum.
source:http://imeysantoso.blogspot.co.id/2017/07/hukum-newton-1-2-3.html
langsung nih artikelnya
Hukum gerak Newton adalah tiga hukum fisika yang menjadi dasar mekanika klasik. Hukum ini menggambarkan hubungan antara gaya yang bekerja pada suatu benda dan gerakyang disebabkannya. Hukum ini telah dituliskan dengan pembahasaan yang berbeda-beda selama hampir 3 abad,[1] dan dapat dirangkum sebagai berikut:
Hukum Pertama: setiap benda akan memiliki kecepatan yang konstan kecuali ada gaya yang resultannya tidak nol bekerja pada benda tersebut.[2][3][4] Berarti jika resultan gaya nol, maka pusat massa dari suatu benda tetap diam, atau bergerak dengan kecepatan konstan (tidak mengalami percepatan). Hal ini berlaku jika dilihat dari kerangka acuan inersial.
Hukum Kedua: sebuah benda dengan massa M mengalami gaya resultan sebesar F akan mengalami percepatan a yang arahnya sama dengan arah gaya, dan besarnya berbanding lurus terhadap F dan berbanding terbalik terhadap M. atau F=Ma. Bisa juga diartikan resultan gaya yang bekerja pada suatu benda sama dengan turunan dari momentum linear benda tersebut terhadap waktu.
Hukum Ketiga: gaya aksi dan reaksi dari dua benda memiliki besar yang sama, dengan arah terbalik, dan segaris. Artinya jika ada benda A yang memberi gaya sebesar F pada benda B, maka benda B akan memberi gaya sebesar –F kepada benda A. F dan –F memiliki besar yang sama namun arahnya berbeda. Hukum ini juga terkenal sebagai hukum aksi-reaksi, dengan F disebut sebagai aksi dan –F adalah reaksinya.
Ketiga hukum gerak ini pertama dirangkum oleh Isaac Newton dalam karyanya Philosophiæ Naturalis Principia Mathematica, pertama kali diterbitkan pada 5 Juli 1687.[5] Newton menggunakan karyanya untuk menjelaskan dan meniliti gerak dari bermacam-macam benda fisik maupun sistem.[6] Contohnya dalam jilid tiga dari naskah tersebut, Newton menunjukkan bahwa dengan menggabungkan antara hukum gerak dengan hukum gravitasi umum, ia dapat menjelaskan hukum pergerakan planet milik Kepler.
Hukum pertama Newton[sunting | sunting sumber]
Berkas:First law.ogv
Walter Lewin menjelaskan hukum pertama Newton.(MIT Course 8.01)[10]
Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Hukum I: Setiap benda akan mempertahankan keadaan diam atau bergerak lurus beraturan, kecuali ada gaya yang bekerja untuk mengubahnya.[11]
Hukum ini menyatakan bahwa jika resultan gaya (jumlah vektor dari semua gaya yang bekerja pada benda) bernilai nol, maka kecepatan benda tersebut konstan. Dirumuskan secara matematis menjadi:
{\displaystyle \sum \mathbf {F} =0\Rightarrow {\frac {d\mathbf {v} }{dt}}=0.}
Artinya :
Sebuah benda yang sedang diam akan tetap diam kecuali ada resultan gaya yang tidak nol bekerja padanya.
Sebuah benda yang sedang bergerak, tidak akan berubah kecepatannya kecuali ada resultan gaya yang tidak nol bekerja padanya.
Hukum pertama newton adalah penjelasan kembali dari hukum inersia yang sudah pernah dideskripsikan oleh Galileo. Dalam bukunya Newton memberikan penghargaan pada Galileo untuk hukum ini. Aristotelesberpendapat bahwa setiap benda memilik tempat asal di alam semesta: benda berat seperti batu akan berada di atas tanah dan benda ringan seperti asap berada di langit. Bintang-bintang akan tetap berada di surga. Ia mengira bahwa sebuah benda sedang berada pada kondisi alamiahnya jika tidak bergerak, dan untuk satu benda bergerak pada garis lurus dengan kecepatan konstan diperlukan sesuatu dari luar benda tersebut yang terus mendorongnya, kalau tidak benda tersebut akan berhenti bergerak. Tetapi Galileo menyadari bahwa gaya diperlukan untuk mengubah kecepatan benda tersebut (percepatan), tetapi untuk mempertahankan kecepatan tidak diperlukan gaya. Sama dengan hukum pertama Newton : Tanpa gaya berarti tidak ada percepatan, maka benda berada pada kecepatan konstan.
Hukum kedua Newton[sunting | sunting sumber]
Walter Lewin menjelaskan hukum dua nuwton menggunakan gravitasi pada contohnya.
(MIT OCW)[12]
Hukum kedua menyatakan bahwa total gaya pada sebuah partikel sama dengan banyaknya perubahan momentum linier p terhadap waktu :
{\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}},}
Karena hukumnya hanya berlaku untuk sistem dengan massa konstan,[13][14][15] variabel massa (sebuah konstan) dapat dikeluarkan dari operator diferensialdengan menggunakan aturan diferensiasi. Maka,
{\displaystyle \mathbf {F} =m\,{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}=m\mathbf {a} ,}
Dengan F adalah total gaya yang bekerja, m adalah massa benda, dan a adalah percepatan benda. Maka total gaya yang bekerja pada suatu benda menghasilkan percepatan yang berbanding lurus.
Massa yang bertambah atau berkurang dari suatu sistem akan mengakibatkan perubahan dalam momentum. Perubahan momentum ini bukanlah akibat dari gaya. Untuk menghitung sistem dengan massa yang bisa berubah-ubah, diperlukan persamaan yang berbeda.
Sesuai dengan hukum pertama, turunan momentum terhadap waktu tidak nol ketika terjadi perubahan arah, walaupun tidak terjadi perubahan besaran. Contohnya adalah gerak melingkar beraturan. Hubungan ini juga secara tidak langsung menyatakan kekekalan momentum: Ketika resultan gaya yang bekerja pada benda nol, momentum benda tersebut konstan. Setiap perubahan gaya berbanding lurus dengan perubahan momentum tiap satuan waktu.
Hukum kedua ini perlu perubahan jika relativitas khusus diperhitungkan, karena dalam kecepatan sangat tinggi hasil kali massa dengan kecepatan tidak mendekati momentum sebenarnya.
Impuls[sunting | sunting sumber]
Impuls J muncul ketika sebuah gaya F bekerja pada suatu interval waktu Δt, dan dirumuskan sebagai[16][17]
{\displaystyle \mathbf {J} =\int _{\Delta t}\mathbf {F} \,\mathrm {d} t.}
Impuls adalah suatu konsep yang digunakan untuk menganalisis tumbukan.[18]
Sistem dengan massa berubah[sunting | sunting sumber]
Sistem dengan massa berubah, seperti roket yang bahan bakarnya digunakan dan mengeluarkan gas sisa, tidak termasuk dalam sistem tertutup dan tidak dapat dihitung dengan hanya mengubah massa menjadi sebuah fungsi dari waktu di hukum kedua.[14] Alasannya, seperti yang tertulis dalam An Introduction to Mechanics karya Kleppner dan Kolenkow, adalah bahwa hukum kedua Newton berlaku terhadap partikel-partikel secara mendasar.[15] Pada mekanika klasik, partikel memiliki massa yang konstant. Dalam kasus partikel-partikel dalam suatu sistem yang terdefinisikan dengan jelas, hukum Newton dapat digunakan dengan menjumlahkan semua partikel dalam sistem:
{\displaystyle \mathbf {F} _{\mathrm {total} }=M\mathbf {a} _{\mathrm {pm} }}
dengan Ftotal adalah total gaya yang bekerja pada sistem, M adalah total massa dari sistem, dan apm adalah percepatan dari pusat massa sistem.
Sistem dengan massa yang berubah-ubah seperti roket atau ember yang berlubang biasanya tidak dapat dihitung seperti sistem partikel, maka hukum kedua Newton tidak dapat digunakan langsung. Persamaan baru digunakan untuk menyelesaikan soal seperti itu dengan cara menata ulang hukum kedua dan menghitung momentum yang dibawa oleh massa yang masuk atau keluar dari sistem:[13]
{\displaystyle \mathbf {F} +\mathbf {u} {\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}}
dengan u adalah kecepatan dari massa yang masuk atau keluar relatif terhadap pusat massa dari objek utama. Dalam beberapa konvensi, besar (u dm/dt) di sebelah kiri persamaan, yang juga disebut dorongan, didefinisikan sebagai gaya (gaya yang dikeluarkan oleh suatu benda sesuai dengan berubahnya massa, seperti dorongan roket) dan dimasukan dalam besarnya F. Maka dengan mengubah definisi percepatan, persamaan tadi menjadi
{\displaystyle \mathbf {F} =m\mathbf {a} .}
Hukum ketiga Newton[sunting | sunting sumber]
Hukum Ketiga Newton. Para pemain sepatu luncur es memberikan gaya pada satu sama-lain dengan besar yang sama tetapi berlawanan arah.
Berkas:Thirdlaw.ogv
Penjelasan hukum ketiga Newton.[19]
“ Lex III: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi. ”
“ Hukum ketiga : Untuk setiap aksi selalu ada reaksi yang sama besar dan berlawanan arah: atau gaya dari dua benda pada satu sama lain selalu sama besar dan berlawanan arah. ”
Benda apapun yang menekan atau menarik benda lain mengalami tekanan atau tarikan yang sama dari benda yang ditekan atau ditarik. Kalau anda menekan sebuah batu dengan jari anda, jari anda juga ditekan oleh batu. Jika seekor kuda menarik sebuah batu dengan menggunakan tali, maka kuda tersebut juga "tertarik" ke arah batu: untuk tali yang digunakan, juga akan menarik sang kuda ke arah batu sebesar ia menarik sang batu ke arah kuda.
Hukum ketiga ini menjelaskan bahwa semua gaya adalah interaksi antara benda-benda yang berbeda,[20] maka tidak ada gaya yang bekerja hanya pada satu benda. Jika benda A mengerjakan gaya pada benda B, benda B secara bersamaan akan mengerjakan gaya dengan besar yang sama pada benda A dan kedua gaya segaris. Seperti yang ditunjukan di diagram, para peluncur es (Ice skater) memberikan gaya satu sama lain dengan besar yang sama, tetapi arah yang berlawanan. Walaupun gaya yang diberikan sama, percepatan yang terjadi tidak sama. Peluncur yang massanya lebih kecil akan mendapat percepatan yang lebih besar karena hukum kedua Newton. Dua gaya yang bekerja pada hukum ketiga ini adalah gaya yang bertipe sama. Misalnya antara roda dengan jalan sama-sama memberikan gaya gesek.
Secara sederhananya, sebuah gaya selalu bekerja pada sepasang benda, dan tidak pernah hanya pada sebuah benda. Jadi untuk setiap gaya selalu memiliki dua ujung. Setiap ujung gaya ini sama kecuali arahnya yang berlawanan. Atau sebuah ujung gaya adalah cerminan dari ujung lainnya.
Secara matematis, hukum ketiga ini berupa persamaan vektor satu dimensi, yang bisa dituliskan sebagai berikut. Asumsikan benda A dan benda B memberikan gaya terhadap satu sama lain.
{\displaystyle \sum \mathbf {F} _{a,b}=-\sum \mathbf {F} _{b,a}}
Dengan
Fa,b adalah gaya-gaya yang bekerja pada A oleh B, dan
Fb,a adalah gaya-gaya yang bekerja pada B oleh A.
Newton menggunakan hukum ketiga untuk menurunkan hukum kekekalan momentum,[21] namun dengan pengamatan yang lebih dalam, kekekalan momentum adalah ide yang lebih mendasar (diturunkan melalui teorema Noether dari relativitas Galileo dibandingkan hukum ketiga, dan tetap berlaku pada kasus yang membuat hukum ketiga newton seakan-akan tidak berlaku. Misalnya ketika medan gaya memiliki momentum, dan dalam mekanika kuantum.
jadi sekian dulu blogku kali ini
SEE YOU NEXT TIME😄😄👋👋source:http://imeysantoso.blogspot.co.id/2017/07/hukum-newton-1-2-3.html
Gaya dan Resultan Gaya
Resultan Gaya
Resultan gaya merupakan besaran vektor. Keseluruhan gaya yang diberikan pada suatu benda dapat diganti oleh sebuah gaya yang disebut resultan gaya. Gaya yang bekerja dengan arah yang sama akan saling menguatkan. Sedangkan, gaya yang bekerja dengan arah berlawanan akan saling melemahkan.
Kenyataannya kekuatan mendorong tiga orang pada arah yang sama lebih besar jika dibanding dua orang dan lebih kuat dibanding kekuatan seorang. Jadi gaya dorong tiga orang tersebut dapat diganti dengan sebuah gaya yang disebut resultan gaya. Bila arah dorongan ketiga orang itu sama, gaya dorong makin besar, tetapi jika arah gaya dorong salah satu melawan dua lainnya, maka gaya dorong mengecil.Resultan Gaya
Resultan Gaya
Jika kita tidak sanggup untuk mendorong suatu benda yang akan kita pindahkan, tentunya kita akan meminta bantuan orang lain untuk mendorong bersama benda tersebbut itu dari arah yang sama. Dengan demikian, benda tersebut akan terasa lebih ringan dan mudah untuk dipindahkan. Tapi, jika kita dan teman kita mendorong dari arah yang berlawanan, benda tersebut akan terasa lebih berat, dan mungkin tidak akan berpindah. Saat benda tersebut didorong dari arah yang sama, maka gaya yang diberikan teman kita akan memperbesar gaya yang telah kita berikan. Sebaliknya, jika arah dorongan kita berlawanan, maka gaya yang diberikan teman kita akan mengurangi gaya yang kita berikan.
Persamaan Resultan Gaya
Arah resultan gaya adalah arah dari sebuah gaya yang nilainya lebih besar dari gaya yang lainnya. Secara matematis, resultan gaya ditulis :
R = F1 + F2 + F3 + … + Fn
dengan:
R = resultan gaya
F = gaya yang dijumlahkan
n = banyaknya gaya
F = gaya yang dijumlahkan
n = banyaknya gaya
Untuk mempermudah perhitungan, berikan tanda positif untuk gaya yang mengarah ke kanan dan ke atas, serta tanda negatif untuk gaya yang mengarah ke kiri dan ke bawah. Misalkan, pada saat mendorong lemari dengan arah berlawanan, gaya yang kita berikan adalah F1 = 22 N mengarah ke kiri. Sementara, gaya yang teman kita berikan adalah F2 = 20 N mengarah ke kanan.
Sehingga, resultan gaya itu adalah
R = F1 + F2
= (-22 N) + 20 N
= (-2 N)
= (-22 N) + 20 N
= (-2 N)
Diperoleh resultan gaya (-2 N). Artinya, besar resultan gaya adalah 2 N dan arahnya sama dengan arah F1, yaitu ke kiri.
Benda berada pada keadaan seimbang atau benda tidak akan bergerak (diam). Jika resultan gaya (R) yang bekerja pada suatu benda sama dengan nol.
source:http://fisikazone.com/resultan-gaya/
source:http://fisikazone.com/resultan-gaya/
Gerak Lurus Berubah Beraturan(GLBB)
Gerak Lurus Berubah Beraturan
Gerak lurus berubah beraturan (GLBB) adalah gerak benda dalam lintasan garis lurus dengan percepatan tetap. Jadi, ciri utama GLBB adalah bahwa dari waktu ke waktu kecepatan benda berubah, semakin lama semakin cepat/lambat...sehingga gerakan benda dari waktu ke waktu mengalami percepatan/perlambatan. Dalam artikel ini, kita tidak menggunakan istilah perlambatan untuk gerak benda diperlambat. Kita tetap saja menamakannya percepatan, hanya saja nilainya negatif. Jadi perlambatan sama dengan percepatan negatif.
Contoh sehari-hari GLBB adalah peristiwa jatuh bebas. Benda jatuh dari ketinggian tertentu di atas permukaan tanah. Semakin lama benda bergerak semakin cepat. Kini, perhatikanlah gambar di bawah yang menyatakan hubungan antara kecepatan (v) dan waktu (t) sebuah benda yang bergerak lurus berubah beraturan dipercepat.
vt = kecepatan akhir (m/s)
a = percepatan
t = selang waktu (s)
Perhatikan bahwa selama selang waktu t , kecepatan benda berubah dari vo menjadi vt sehingga kecepatan rata-rata benda dapat dituliskan:
S = jarak yang ditempuh
seperti halnya dalam GLB (gerak lurus beraturan) besarnya jaraktempuh juga dapat dihitung dengan mencari luasnya daerah dibawah grafik v - t
Bila dua persamaan GLBB di atas kita gabungkan, maka kita akan dapatkan persamaan GLBB yang ketiga.....
2. Contoh-Contoh GLBB
a. Gerak Jatuh Bebas
Ciri khasnya adalah benda jatuh tanpa kecepatan awal (vo = nol). Semakin ke bawah gerak benda semakin cepat.Percepatan yang dialami oleh setiap benda jatuh bebas selalu sama, yakni sama dengan percepatan gravitasi bumi (a = g) (besar g = 9,8 m/s2 dan sering dibulatkan menjadi 10 m/s2)
Rumus gerak jatuh bebas ini merupakan pengembangan dari ketiga rumus utama dalam GLBB seperti yang telah diterangkan di atas dengan modifikasi : s (jarak) menjadi h (ketinggian) dan vo = 0 serta percepatan (a) menjadi percepatan grafitasi (g).
coba kalian perhatikan rumus yang kedua....dari ketinggian benda dari atas tanah (h) dapat digunakan untuk mencari waktu yang diperlukan benda untuk mencapai permukaan tahah atau mencapai ketinggian tertentu... namun ingat jarak dihitung dari titik asal benda jatuh bukan diukur dari permukaan tanah
sebagai contoh : Balok jatuh dari ketinggian 120 m berapakah waktu saat benda berada 40 m dari permukaan tanah?
jawab : h = 120 - 40 = 80 m
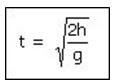
t = 4 s
2. Gerak Vertikal ke Atas
 Selama bola bergerak vertikal ke atas, gerakan bola melawan gaya gravitasi yang menariknya ke bumi. Akhirnya bola bergerak diperlambat. Akhirnya setelah mencapai ketinggian tertentu yang disebut tinggi maksimum (h max), bola tak dapat naik lagi. Pada saat ini kecepatan bola nol (Vt = 0). Oleh karena tarikan gaya gravitasi bumi tak pernah berhenti bekerja pada bola, menyebabkan bola bergerak turun. Pada saat ini bola mengalami jatuh bebas....
Selama bola bergerak vertikal ke atas, gerakan bola melawan gaya gravitasi yang menariknya ke bumi. Akhirnya bola bergerak diperlambat. Akhirnya setelah mencapai ketinggian tertentu yang disebut tinggi maksimum (h max), bola tak dapat naik lagi. Pada saat ini kecepatan bola nol (Vt = 0). Oleh karena tarikan gaya gravitasi bumi tak pernah berhenti bekerja pada bola, menyebabkan bola bergerak turun. Pada saat ini bola mengalami jatuh bebas....
Jadi bola mengalami dua fase gerakan. Saat bergerak ke atas bola bergerak GLBB diperlambat (a = - g) dengan kecepatan awal tertentu lalu setelah mencapai tinggi maksimum bola jatuh bebas yang merupakan GLBB dipercepat dengan kecepatan awal nol.
Pada saat benda bergerak naik berlaku persamaan :
vo = kecepatan awal (m/s)
g = percepatan gravitasi
t = waktu (s)
vt = kecepatan akhir (m/s)
h = ketinggian (m)
3. Gerak Vertikal ke Bawah
Berbeda dengan jatuh bebas, gerak vertikal ke bawah yang dimaksudkan adalah gerak benda-benda yang dilemparkan vertikal ke bawah dengan kecepatan awal tertentu. Jadi seperti gerak vertikal ke atas hanya saja arahnya ke bawah. Sehingga persamaan-persamaannya sama dengan persamaan-persamaan pada gerak vertikal ke atas, kecuali tanda negatif pada persamaan-persamaan gerak vertikal ke atas diganti dengan tanda positif.
3. Rangkuman GLB dan GLBB
Demikian artikel tulisan saya tentang Gerak Lurus Beraturan (GLB) dan Gerak Lurus Berubah Beraturan (GLBB). Semoga bermanfaat. Terima Kasih.
source:http://pengetahuan-olandsky.blogspot.co.id/2013/08/gerak-lurus-beraturan-glb-dan-gerak.html















